Euler’s Formula: a Calculus Approach
Euler’s Formula, Logarithm of a Negative Number, and Complex Exponentiation
Euler’s formula is an important mathematical identity that was discovered in 1740 by Swiss mathematician Leonhard Euler. Euler, who is regarded today as one of the greatest mathematicians of all time, authored numerous mathematical papers and made groundbreaking discoveries and contributions in mathematics. One of the most well-known results from Euler is his famous equation that is derived in this paper:
It is one of the most important, versatile and profound mathematical formulas in mathematics. The equation was literally voted in a 1988 poll as the most beautiful mathematical2 expression ever derived.
Several mathematicians were close to deriving the formula before Euler, but the equation did not take its form as it is in today until Euler used De Moivre’s theorem3 to derive it in his pre-calculus book. Its importance was not discovered until mathematicians began to realize its versatility and significance in other areas of mathematics4.
I independently discovered this derivation by accident while I was taking a calculus II course. My goal was not to derive an identity, but to find different methods of integration. The idea of substituting complex variables interested me, and I soon found that integrating certain functions with complex variables lead to the same equation: Euler’s formula. Here is the original way I derived the formula.
Remark
Riemann integrals5 are defined for real numbers, and including complex numbers6 may seem illegal. One must go back through real analysis and confirm that the complex numbers satisfy results that the real numbers satisfy in order to use specific theorems established in real analysis. In other words, using complex numbers is mathematically illegal until its legality is proven, which I have already completed in a formal proof of this using the Jacobian for making a transformation.
I’ve made an extensive search across the internet to see if this derivation has been discovered, and I have come up empty. That is why I maintain this to be my own work.
Consider the indefinite integral
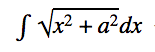 where
where ![]() .
.
The function inside of the integral is the upper half of an arbitrary hyperbola8.
Real derivation
Using trigonometric substitution, substitute the expression ![]() where
where ![]()
The integral then becomes

Given the trigonometric identity ![]() we can substitute the expression to give an even simpler integral.
we can substitute the expression to give an even simpler integral.
The integral![]() has a lengthy derivation and it is omitted.
has a lengthy derivation and it is omitted.
Through integration by parts, the most general antiderivative (where c=0) is equivalent to
![]() However, the reason why the absolute value is added to the antiderivative is to avoid the natural logarithm of a negative number. This is going to be defined, but in order to define it, the absolute value symbol must first be removed.
However, the reason why the absolute value is added to the antiderivative is to avoid the natural logarithm of a negative number. This is going to be defined, but in order to define it, the absolute value symbol must first be removed.
Using the expression
![]() and substituting it, the following is obtained:
and substituting it, the following is obtained:
![]() To change the variables back into the xy-plane, one must derive different trigonometric expressions in terms of x. A common way to do this is to use a triangle to better visualize the expressions9.
To change the variables back into the xy-plane, one must derive different trigonometric expressions in terms of x. A common way to do this is to use a triangle to better visualize the expressions9. 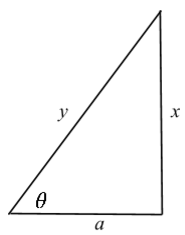
If ![]() then
then ![]() which explains the structure of the triangle.
which explains the structure of the triangle.
Using the pythagorean theorem, We can see that
![]()
Finally, the antiderivative may be expressed in terms of x.
Complex derivation
This is what derives the interesting results. The derivation of the integral involves a substitution where the variables are transformed to the complex plane.
Using trigonometric substitution, the expression ![]() can be substituted into the integral
can be substituted into the integral
Omitting the derivation, ![]() which implies
which implies
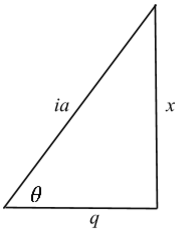
In order to transfer back to rectangular coordinates, another triangle is used again.
Using ![]() to derive the triangle, we can find an expression for
to derive the triangle, we can find an expression for![]()
The Pythagorean theorem can be used to find q.
Substituting the new expression for q to derive 
Transferring back to rectangular coordinates,
Thus, we have two expressions from the same integral, one from the real plane and one from the complex plane. Equating the two expressions, we have
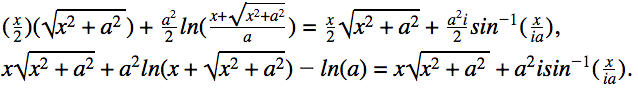 Notice that if we set a=1, we get
Notice that if we set a=1, we get
![]()
![]() Thus, the logarithm of a negative number is a complex number, leading to what is known as one of the most beautiful mathematical expressions ever derived:
Thus, the logarithm of a negative number is a complex number, leading to what is known as one of the most beautiful mathematical expressions ever derived:
This gives a definition for the logarithm of a negative number.
Continuing with the derivation, we are met with the equation
![]() Notice that
Notice that ![]() can be subtracted from both sides,
can be subtracted from both sides,
![]() Using the fact that
Using the fact that ![]() and
and ![]() we have that
we have that![]() and raising this equation to the power of e we obtain Euler’s formula:
and raising this equation to the power of e we obtain Euler’s formula:
which is the definition for complex exponentiation.
The idea behind this can be thought of in terms of linear algebra. It can first be shown that the complex plane forms a vector space. Then it can be shown that the transformation from the real plane into the complex plane ![]() is linear, one-to-one, and onto, if the transformation matrix A is given by the basis vectors of the complex plane10. Not surprisingly, the transformation has no effect on the area. That is why when the two integrals are equated, despite their differing transformations and derivations, an identity is obtained.
is linear, one-to-one, and onto, if the transformation matrix A is given by the basis vectors of the complex plane10. Not surprisingly, the transformation has no effect on the area. That is why when the two integrals are equated, despite their differing transformations and derivations, an identity is obtained.
Notes:
- In Euler’s formula, e is Euler’s constant, 2.71828…; i is the imaginary unit
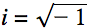 ; is the independent variable; and
; is the independent variable; and 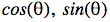 are the trigonometric functions. For our purposes, we shall consider
are the trigonometric functions. For our purposes, we shall consider 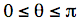 or
or 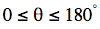
- Euler’s formula is the most fundamental identity of all identities. It is the connection between logarithms and inverse
 trigonometric functions, the connection between the exponential function
trigonometric functions, the connection between the exponential function 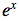 and the complex trigonometric functions (i.e.,
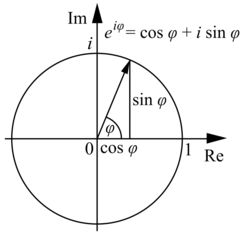
and the complex trigonometric functions (i.e., , and it is a primary focus of study in complex analysis. It is very useful tool in differentiation, as it can be used to simplify equations through substitutions. The formula also has numerous implications upon the area of Fourier Analysis. The most interesting part, however, is to note that it is the general equation of a circle in the complex plane (the plane on the left is the complex plane). One of the most prominent theoretical physicists of the 20th century, Richard Feynman, was quoted while describing the formula as a “jewel” and “the most remarkable formula in mathematics.
, and it is a primary focus of study in complex analysis. It is very useful tool in differentiation, as it can be used to simplify equations through substitutions. The formula also has numerous implications upon the area of Fourier Analysis. The most interesting part, however, is to note that it is the general equation of a circle in the complex plane (the plane on the left is the complex plane). One of the most prominent theoretical physicists of the 20th century, Richard Feynman, was quoted while describing the formula as a “jewel” and “the most remarkable formula in mathematics.
- See http://eulerarchive.maa.org/hedi/HEDI-2007-08.pdf for a historical treatment of Euler’s formula, in addition to the original way he discovered it.
- As with many formulas, the expression has numerous philosophical implications. The expression can be seen as the intersection of algebra, geometry, arithmetic, and the complex and real numbers. It is also notable because it has the two most important and famous constants of mathematics.
 is from geometry, e is from algebra, 1 and 0 are the two most basic real numbers, i is from the complex numbers.
is from geometry, e is from algebra, 1 and 0 are the two most basic real numbers, i is from the complex numbers.
- A Riemann integral is a method of finding the area under a curve using very thin rectangles to approximate the area. The integrals in the derivation, however, are called indefinite integrals. In rough terms, finding the indefinite integral of a function in the xy-plane is equivalent to finding a formula for its area under the curve. Note: In all of the indefinite integral expressions, I omit all constants and assume the most general formulas with c=0.
- Real numbers are simply everyday numbers (e.g., 1, 2, 0.5, 0.00005, 3.33…,
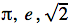 ). Complex numbers are the set of numbers
). Complex numbers are the set of numbers 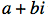 where a, b are real numbers (Ex: 2+0.0055432i, 3+5i are complex numbers).
where a, b are real numbers (Ex: 2+0.0055432i, 3+5i are complex numbers).
- The hyperbola in question looks like the following:
- In calculus, trigonometric substitution is used to simplify expressions and to ease the obtainment of the indefinite integral. It simply involves momentarily transforming the expressions into another coordinate system, and transferring back to the original coordinate system after the integration has been completed. The purpose of the triangle is used in a non-rigorous manner to find different trigonometric expressions.
- In a rough manner, one could lay the real plane on top of the complex plane so that they would never overlap each other and they would be exact replicas. Each and every point is mapped to one and only one point when the transformation matrix is given by the basis vectors of the complex plane.




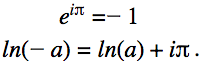






Robert Brack • Mar 15, 2016 at 1:01 pm
Very cool article to see connection between e, i, 1, and pi.